Movimiento bajo fuerza constante en mecánica cuántica

Movimiento bajo fuerza constante en mecánica cuántica

En mecánica cuántica no se puede hablar de trayectorias ya que la posición de la partícula no puede determinarse con precisión arbitraria, por lo que sólo existen análogos cuánticos imperfectos del movimiento rectilíneo clásico. El equivalente cuántico más simple de movimiento uniformemente acelerado es el de una partícula cuántica (no relativista y sin espín) en un campo de fuerzas conservativo en el que la energía potencial es una función lineal de la coordenada.
-\frac{\hbar^2}{2m} \frac{\part^2 \Psi}{\part x^2} - xF \psi(x,t) = i\frac{\part \Psi(x,t)}{\part t}
La solución general de esta ecuación puede escribirse como transformada de Fourier del conjunto de soluciones de la ecuación estacionaria:
\Psi(x,t)= \left(\frac{m}{\hbar^2F^2}\right)^{1/3} \int_{-\infty}^{+\infty} A_E\ \hat{\psi}(x;E)e^{-iEt/\hbar}\ dE
Donde \scriptstyle A_E la amplitud es una función de la energía que debe escogerse para satisfacer las condiciones iniciales y la función \scriptstyle \hat{\psi}(x;E) en el integrando debe ser solución de la ecuación de Schrödinger estacionaria:
-\frac{\hbar^2}{2m} \frac{\part^2 \psi_E}{\part x^2} - xF \psi_E(x) = E\psi_E(x), \qquad \psi_E(x):= \hat{\psi}(x;E)
Donde:
\hbar\, es la constante de Planck racionalizada.
m\, es la masa de la partícula.
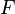F\, es la fuerza que se ejerce sobre la partícula.
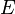E\, es la energía de un estado estacionario del hamiltoniano cuántico.
Haciendo el cambio de variable:
\bar{x} = - \left( \frac{2m}{\hbar^2 F} \right)^{1/3} (E+xF)
Entonces la ecuación (*) equivale a la ecuación:
\frac{d^2 \psi_E(\bar{x}) }{d\bar{x}^2} - \bar{x} \psi_E(\bar{x}) =0
Que es la ecuación de Airy, por lo que la solución general de la ecuación de Schrödinger queda en términos de funciones Airy:
\psi_E(x)=A \mathrm{Ai}(\bar{x}) + B \mathrm{Bi}(\bar{x})
Por consideraciones físicas B = 0, ya que en caso contrario la anterior función no sería acotada.
Nótese que la ecuación anterior tiene solución para cualquier valor de E y por tanto los estados energéticos posibles de una partícula tienen un espectro continuo (a diferencia de lo que pasa para otros sistemas cuánticos con niveles de energía discretos).

No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)